Note: There was a bit of doubt about the airmass units on my part. This has now been resolved and milligrams/stroke is the winner.
The first "secret' of the Td5 engine maps is that nothing is quite what it seems at first glance.
If you look at the live data from a Nanocom you are presented with individual sensor readings for MAF and MAP, and the assumption is usually the engine is using MAF for fuelling and the MAP readings for boost. In fact, the reality is a bit more complex.
EU2 motors use data from the MAP and IAT sensors to calculate the airmass in milligrams within each cylinder on each intake stroke (mg/stroke).
For EU3 motors the data from the MAF sensor and the Engine Speed in RPM are used to determine the airmass in milligrams within each cylinder on each intake stroke (mg/stroke). As a backup EU3 motors will fail over to MAP/IAT based calculations if the MAF is outside a specific range but more on this later.
The airmass figures indicates is the mass of air within the cylinder at the end of the intake stroke. This is a critical piece of information for the engine as the amount of fuel injected depends on a combination of the amount of air within the cylinder and the speed of the engine
Unfortunately the Nanocom does not give access to the live data for the Airmass parameter, so the only option is to use the MAP/IAT and MAF/RPM data to calculate the airmass value. Strictly speaking airmass value based on the MAF reading is not calculated - Mass Air Flow is divided down to reflect the amount of air drawn into the cylinder on each intake stroke.
I've posted up the math to calculate airmass to several forums as a method of comparing the MAP and MAF readings for diagnostic but the significance has been elided. I'll run through the calculations again before moving on.
It's important to note that the Nanocom alters the values reported by the ECU to more familiar units. This is fine for some purposes but it does tend to obscure the relationship with engine map parameters. I've added multipliers and conversion from deg C to Kelvin (+ 273.2) as necessary.
Speed-Density: Airmass from MAP and IAT
The calculation used for this conversion is based on the Ideal Gas Law, which can be used to calculate the amount of air present in the cylinder given the volume, absolute pressure and inlet air temperature. This method is commonly known as speed-density, and RAVE makes passing reference to this in the Td5 ECU section of the D2 workshop manual.
The formula for the Ideal Gas Law is PV = nRT
- P is absolute pressure
- V is volume in litres
- n is the amount of substance of a gas - also known molar mass. For air this is approx. 28.97g/mole
- R is the universal gas constant
- T is absolute temperature in Kelvin.
When all the parameters are known - as in the case of the ECU - the formula can be rewritten as`
n = PV/RT
Airmass in grams can then be found by multiplying n by n(air).
The Td5 ECU applies this method to calculate Airmass based on the MAP and IAT readings:
airmass = (MAP * Cylinder Volume in cc * Molar Mass air (g/mole)) / (IAT(K) * R)
A point of clarification on the ECU units. The MC68336 processor used in the ECU does not provide hardware support for floating point math, making working with decimal fraction extremely slow. To keep the calculations fast integer math is used, and the number scaled to give the required precision. If accuracy to 1 decimal place is required the number is multiplied by 10. The value for R requires three decimal places accuracy and is multiplied by 1000.
The internal values used by the ECU are:
- MAP = kPa * 100 (or milliBar * 10)
- IAT = Kelvin * 10
- Cyl Volume = 498
- n(air) = 28980
- R = 8314
To use this with Nanocom logs I substitute the ECU constants used for the fixed elements, and scale to match the ECU internal values for MAP and IAT. The Nanocom alters the raw log values to a more user friendly format, so this requires converting IAT from Celsius back to Kelvin, and multiplying MAP by 100.
airmass = (MAP * 100 * 498 * 28980) / ((IAT+273.2) * 10 * 8314)
or
airmass = (MAP * 10 * 498 * 28980) / (IAT+273.2) * 8314)
The value is close to the ECU calculated value but suffers from a small amount of time smearing due to the engine conditions changing between sensor requests. As can be seen below the relationship between ECU values and the value calculated from MAP and IAT is pretty close, as shown by the straight 45 degree line.
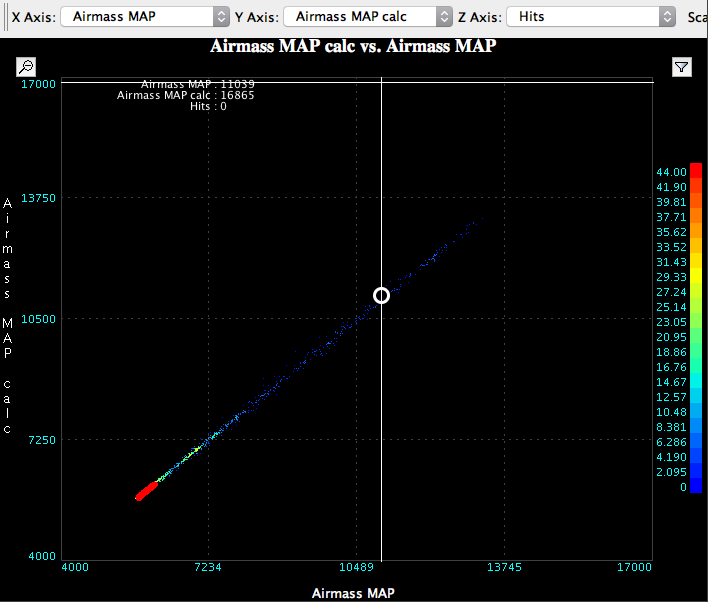
MAF and RPM
The MAF airmass calculation is simplified because the MAF reading is already provides the airmass entering the engine given in kg/Hr. Conversion from kg/hr -> g/min is done by multiplying by 1000 and dividing by 60. The intake stroke of each cylinder occur once every 2 revolutions, so the airmass is divided by 5/2 to determine the amount per cylinder. The ECU code combines these to simplify calculation:
33.333 = (1000 * 2) / 60
The final code used in all variants of the Td5 ECU is:
airmass = (MAF * 33333) / (RPM * 5)
Note that the decimal point of the constant is shifted right three places to retain precision in integer math. The ECU representation of the MAF vale has it's decimal point shifted one place to the right. This is significant when reading the ECU maps as the map values use these fixed point numbers.
To confirm the magnitude of the units, lets apply this to the Nanocom values at a typical idle reading of 60kgHr/ 760rpm.
airmass(g) = 60 * 33.333 / 760 *5 airmass = 0.5263g or 526.3mg
And at 680kg/Hr/ 3500rpm airmass = 1.2952g or 1295.2mg
Referring to 0.5623g airmass feels pretty clumsy, so my preference is to use mg.
Looking at log data the time scatter is far more evident in the MAF airmass from the same log data as the MAP airmass. This is evident in the spread of values above and below a 45 degree line.
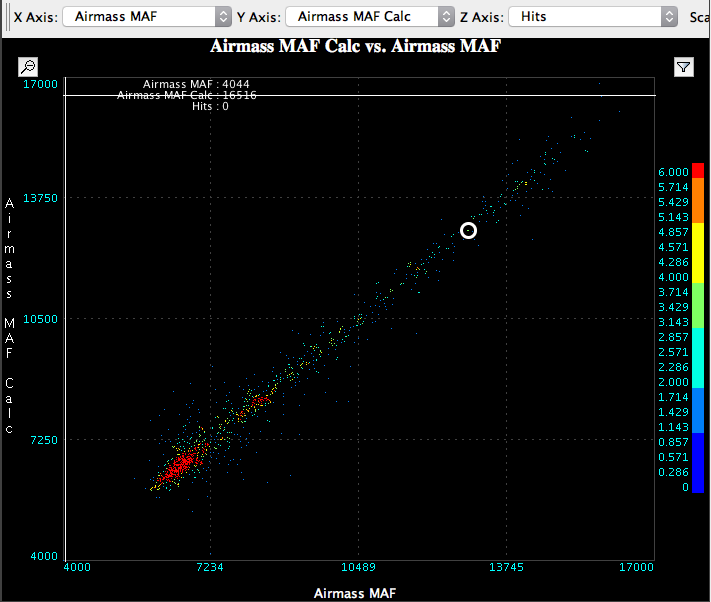
Bonus diagnostic content.
Because we are calculating two values measuring the same quantity, it is possible to check sensor health by comparing the two readings using a scatter plot. If the sensors are behaving correctly there is a linear relationship between the airmass values. If one of the sensors is misreading you tend to see distinct curvature or complete breakdown of the relationship.
